BOOLE, UN PROBLEMA Y UN BUCLE

BOOLE, UN PROBLEMA Y UN BUCLE

Reconozco que este escrito puede ser algo árido, pero es que se cumplen ahora, el día 2 de noviembre, 210 años del nacimiento de George Boole, el matemático británico que hizo contribuciones significativas en el campo de la lógica y las matemáticas. Antes de Boole, la lógica era una rama de la Filosofía, heredada de Aristóteles; pero él fue el primero en convertirla en una ciencia matemática, usando símbolos y ecuaciones para representar el razonamiento.

Boole nació en Lincoln, Inglaterra, en 1815, en una familia muy humilde. Fue autodidacta total; no pudo asistir a la universidad y aprendió latín, griego y matemáticas por su cuenta. Nunca tuvo formación académica, pero comenzó a trabajar como maestro a los 16 años y estableció su propia escuela. En 1849 fue nombrado profesor de matemáticas en la universidad de Cork, en Irlanda, gracias a sus méritos científicos.

Contrajo matrimonio con Mary Everest, sobrina del geógrafo que dio nombre al monte Everest. Era una mujer muy culta y espiritual. Había sido su alumna por correspondencia, con cartas donde exponía sus dudas sobre lógica y filosofía. Decía que no se había enamorado del hombre de “carne y hueso”, sino de la “mente que veía a Dios en las ecuaciones”.

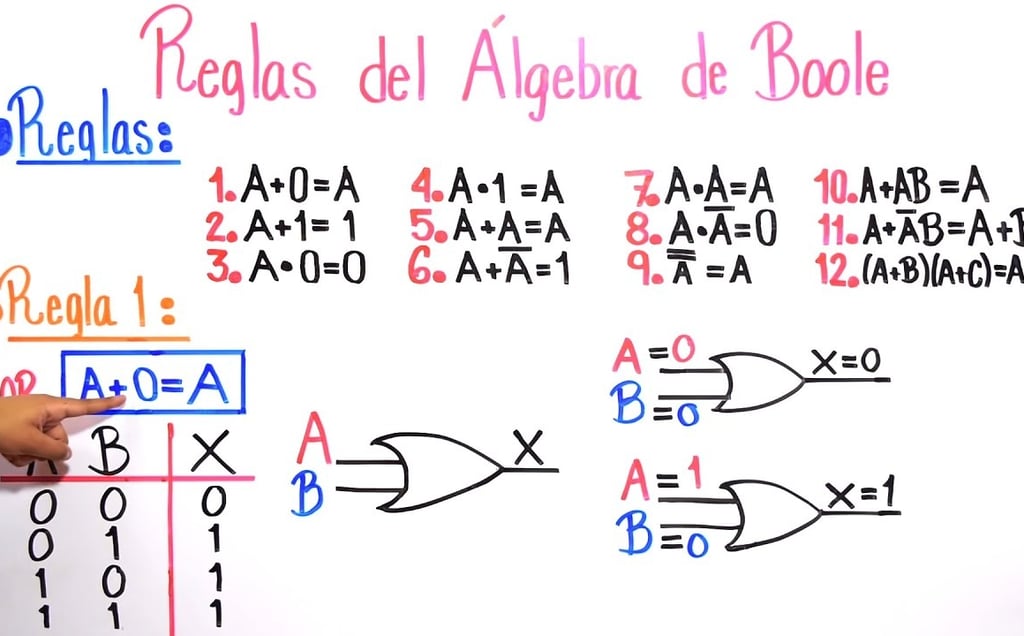
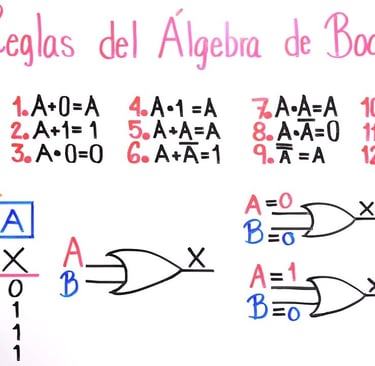
En 1854, Georges Boole escribió su obra maestra: “Una investigación sobre las leyes del pensamiento”. En este libro introdujo lo que hoy se llama “Algebra de Boole”, un sistema en el que las proposiciones se expresan con valores 1 (verdadero) y 0 (falso); lógica que ha servido a Google para desarrollar su sistema de búsquedas, con el famoso "And", "Or" y "Not". Además, este sistema resultó ser la base teórica de los circuitos electrónicos que usan los ordenadores actuales.

El álgebra de Boole es una estructura algebraica que esquematiza las operaciones lógicas, y que abrió el camino a toda la programación actual: desde el código de las aplicaciones del móvil hasta los videojuegos. Esta teoría supuso el nacimiento de la revolución digital.

Boole no tenía ni idea de que su álgebra se aplicaría a las máquinas. Un siglo después, un ingeniero americano se dio cuenta de que los circuitos eléctricos de conmutadores podían representarse con el álgebra de Boole. Esto dio origen a la electrónica digital y, en última instancia, a internet.

El álgebra de Boole se puede utilizar para representar y analizar secuencias binarias como las que se generan en el siguiente problema, que os propongo realizar. Vamos a construir una sucesión de números naturales (enteros positivos). El problema es muy sencillo, de manera que incluso quién sea de "letras", lo puede entender y efectuar, ya que se trata de una secuencia de decisiones lógicas.

Se trata de esta sencilla función "3n + 1". Empezamos por un número cualquiera. Digamos, a manera de ejemplo, que elegimos el número 7. Ese va a ser el primer elemento de nuestra sucesión.

La secuencia es la siguiente: para generar el segundo elemento de la sucesión, hacemos lo siguiente:

-Si el número es par, lo dividimos entre 2.

-Si es impar, aplicamos la función 3n + 1; es decir, lo multiplicamos por 3 y le sumamos 1.

Toda la secuencia se puede escribir como una cadena de operaciones booleanas, que se ejecutan una y otra vez.

En nuestro ejemplo, al haber elegido el 7, como no es par, tenemos que multiplicarlo por 3 y sumarle 1. Es decir, se obtiene el número 22, ya que 3 X 7 = 21 y sumando 1, queda 22. Tenemos entonces los primeros dos elementos de nuestra sucesión: {7, 22}.

Vamos a generar el tercer elemento de la sucesión: como el 22 es un número par, lo dividimos por dos, y obtenemos 11. Ahora ya tenemos {7, 22, 11}. Seguimos. Como 11 es impar, la secuencia dice: “multiplícalo por 3 y súmale 1”. O sea, 3 X 11=33 + 1= 34. Se tiene {7, 22, 11, 34}. Luego, como 34 es par, el próximo elemento de la sucesión se obtiene dividiendo entre 2, y es 17. Y el siguiente es 52. Luego 26. Y después 13. Y sigue 40. Luego 20. (Espero que no os hayáis perdido). Hasta aquí tenemos {7, 22, 11, 34, 17, 52, 26, 13, 40, 20} y seguimos dividiendo entre 2 los números pares, y multiplicando por 3 y sumando 1 a los impares:

{7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1}

Y en el número 1, paramos.

Os invito ahora a que elijáis cualquier otro número para empezar, digamos, por ejemplo, el 24. La sucesión que se tiene es:

{24, 12, 6, 3, 10, 5, 16, 8, 4, 2, 1}

Si ahora elegimos el 100, se sigue:

{100, 50, 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1}

Como podéis ver, todas las sucesiones que elegimos terminan en el número 1.

En realidad, aunque no lo he dicho antes, al llegar al número 1 el proceso se detiene, porque si uno siguiera, entraría en un bucle, ya que, el 1, que es impar, lo multiplicaríamos por 3 y sumamos 1, y pasaría al 4, del 4 al 2 y del 2 otra vez al 1. Por eso, es que cuando al construir la sucesión llegamos al número 1, detenemos el proceso.

Hasta hoy, en todos los ejemplos conocidos siempre se termina la sucesión en el número 1. Pero no se tiene ninguna demostración que pruebe que el resultado siempre es 1 para cualquier número con el que comencemos el ejercicio.

Este problema se conoce con el nombre de “problema 3n + 1”, o también como el “Problema de Collatz”, o “Problema de Syracusa”, o “Problema de Kakutani” o “Algoritmo de Hasse” o “Problema de Ulam”. Como se ve, tiene muchos nombres, pero ninguna solución. Es uno de los problemas más famosos de las matemáticas, precisamente porque es muy fácil de entender, pero nadie ha podido demostrarlo todavía. Es una buena oportunidad para empezar. Sin embargo, es muy poco probable que una persona “lega” tenga las herramientas suficientes para resolverlo.

Estiman los matemáticos que solo habrá unas veinte personas en el mundo capaces de “atacarlo”. Pero eso no significa que, en algún lugar del planeta, por mayor o menor entrenamiento matemático haya alguien más, que se le ocurra una idea que nadie tuvo antes y el problema quede resuelto por una persona que no pertenezca a ese privilegiado grupo de veinte.

Este problema que os acabo de contar se inscribe dentro de una larga lista de problemas que las matemáticas tienen sin resolver aún. Es fácil aceptar esto en otras ciencias. Por ejemplo, la medicina no sabe aún cómo resolver algunas variedades de cáncer o del Alzheimer, por poner un par de ejemplos. La física no tiene aún una “teoría” que integre lo macro con lo micro, ni conoce todas las partículas elementales. La biología no conoce aún cómo funcionan todos los genes ni cuántos son. En fin, estoy seguro que se pueden agregar muchísimos ejemplos más. Las matemáticas tienen su propia lista de problemas sin resolver. Conforme se vayan resolviendo, puede que se abran nuevas puertas a la tecnología y al progreso humano.

Y hablando de “bucles”, tengo que decir que, cuando en informática se habla de "bucles", mucha gente no acaba de comprender qué son. Para quien no conoce el concepto, hay que decir que “bucle” es un término que crearon los informáticos para definir un enredo de los tantos que se han creado y para el que no tienen una explicación sencilla, al encontrarse atrapado en un proceso que se repite una y otra vez. Voy a tratar de explicar este famoso término con un ejemplo. Se dice que un programa de informática “entró en un bucle", cuando ocurre una situación como la siguiente:

El director de una empresa, llama a su secretaria y le dice:

- Mañana hay una reunión en Barcelona, y necesito que me acompañe para que conozca a mis socios. Haga los preparativos del viaje...

La secretaria llama a su marido:
- ¡Oye! Mañana voy a tener que viajar a Barcelona con el director. Tendrás que quedarte solo, querido.

El marido llama a un amigo:
- Mi mujer viaja mañana por asuntos de trabajo a Barcelona; si puedes,

podemos ir a jugar al golf y a comer en el club.

El amigo llama al niño, a quien le da clases particulares diarias:
- Mira, Mañana tengo un problema y no voy a poder ir a darte clase...

El niño llama a su abuelo:
- Oye abuelo: Mañana no tengo clases; mi profesor está ocupado. Así que... ¡Vamos a poder pasar el día juntos en el campo!

El abuelo (que es el director en esta historia) llama a la secretaria:
- Suspenda el viaje a Barcelona; voy a pasar el día con mi nieto en el campo, y no voy a participar en la reunión.

La secretaria llama al marido:
- El director ha cambiado de idea y acaba de cancelar el viaje a Barcelona. No me marcho de viaje.

El marido llama al amigo:
- Oye: No podemos ir mañana a jugar al golf, el viaje de mi mujer se ha cancelado.

El amigo llama al niño de las clases particulares:
- Mira, cambié de planes; mañana sí te voy a dar clases como siempre.

El niño llama al abuelo:
- Abuelo: mi profe me ha dicho que sí podrá darme clases mañana, así que no voy a poder ir al campo contigo.

El abuelo llama a la secretaria:
- Mi nieto me acaba de decir que no va a poder estar conmigo mañana porque tiene clases. Así que continúe con los preparativos del viaje a Barcelona...

La secretaria vuelve a llamar al marido …

¿¿¿Ha quedado claro lo que es un bucle...???

José Antonio Parra Tomás