PRIMOS DE MERSENNE
Descripción de la complejidad e historia que suponen los números primos y dentro de estos el grupo denominado de Mersenne, un grupo muy especial.
JOSÉ ANTONIO PARRA TOMÁS
José Antonio Parra en Asociación la Tortuga de El Charco.
1/18/20256 min read


Parece que hay gente feliz con ello, pero yo no; me siento mal, me siento inquieto. Quizá por mi propia forma de ser, tal vez por educación o genética. ¡Qué sé yo! Sin embargo, me gusta y me llama la atención. Será por el hecho de que, en origen, soy de ciencias, y era muy fácil aceptar que dos más dos son cuatro y que la longitud de la circunferencia es diámetro por pi. Pero, lo único que puedo constatar, lo único que puedo decir ahora mismo es que solo sé que no sé nada, y que lo único que llego a comprender es que me cuesta trabajo asimilar ciertos conceptos. Se sale de mis esquemas.
Y os estaréis preguntando, ¿a qué se refiere? Pues a lo siguiente. Voy a ver si explicándolo, llegó a comprenderlo, a digerirlo.
No sé si alguno habréis leído que el pasado 21 de octubre, GIMPS anunciaba el descubrimiento de un nuevo integrante de la exclusiva lista de los llamados primos de Mersenne, tras seis años esperando desde que se encontró el anterior. GIMPS es un grupo de científicos y matemáticos que se dedican a buscar números primos de Mersenne, y ahora han descubierto un número primo muy grande. Pertenece a esa grupo muy especial de números primos, que es la de los primos de Mersenne (recibieron su nombre del monje francés Marin Mersenne, que estudió estos números hace más de 350 años). Son unos números primos muy particulares. Si queréis encontrar un primo de Mersenne os dejo el siguiente algoritmo, es decir, la receta:
1. Se toma un número primo (llamémosle p).
2. Eleváis 2 al número p, o sea, lo multiplicas por sí mismo p veces.
3. Le restáis uno al resultado.
4. Si el resultado es un número primo, ¡BINGO!, es un primo de Mersenne.
¿Lo vais entendiendo?
Os pongo un ejemplo. Tomad uno de los primeros números primos que hay, por ejemplo, el 3. Eleváis dos “al cubo”, dos por sí mismo tres veces, 2x2x2, os da 8. Le restáis 1, y el resultado es 7. ¿Es primo? Sí. Pues entonces 7 es un primo de Mersenne. Os recuerdo que un número es primo si solo se puede dividir por uno y por sí mismo. El griego Euclides (325-265 a.C.) fue el primero en mencionar la existencia de los números primos (2, 3, 5, 7, 11...). Se sabe que son infinitos, pero a medida que crecen, la distancia que los separa es cada vez mayor y por lo tanto más complicado dar con ellos.
Este grupo de primos de Mersenne se conocía desde la antigüedad, pero solo se conocían los cuatro primeros (3, 7, 31 y 127). De hecho, cuando se descubrió el quinto (en el siglo XV) se llegó a formular que todos los números que salían de hacer los pasos de 1 a 3 anteriores, resultaban número primo partiendo de cualquier número primo p.
El grupo fue creciendo según mejoraban las técnicas de cálculo y se llegó a tener 12 primos de Mersenne en el siglo XIX. Luego creció más con la introducción de los ordenadores.
El que se ha anunciado ahora, octubre de 2024, es el que hace el 52 primo de Mersenne. Y ahora viene lo difícil de asimilar. Para que vayáis haciéndose una idea, os digo que este primo se obtiene cuando elevamos 2 a 136.279.841 y le restamos 1, y el resultado es un número que tiene más de 41 millones de dígitos (en concreto, tiene 41.024.320 dígitos), superando así en más de trece millones de dígitos a su antecesor (el 51, que se descubrió el 21 de diciembre de 2018).
El nuevo primo de Mersenne que se acaba de conocer, y que se designa como M136279841, es el siguiente: M136279841 = 2(elevado a 136279841) -1
Y, como decía antes, tiene más de 41 millones de cifras. Como os he comentado al principio, pienso (y no lo logro) que es muy complicado asimilar el abismal tamaño de un número así, por lo que voy a poner un ejemplo para intentar ayudar a dicha asimilación: imaginad que tenéis el presupuesto del Estado, es decir, un billón de euros. Una cantidad enorme, ¿verdad? Bien, pues el número “un billón” tiene 13 dígitos: 1.000.000.000.000.
Así que imaginad lo gigantesco que es un número de más de ¡¡41 millones de dígitos!! (Empieza por 8816943275038332655539391003…, y termina muuuuuchoo después).
Puede que me digáis aquello de: ¿Y a mí qué me importa esos números?
Tened en cuenta que la mayoría de los sistemas que encriptan los mensajes a través de redes se apoyan en la factorización de números grandes, o sea, pueden emplearse para codificar cualquier tipo de información de manera segura; es un sistema que utilizan los bancos en los números de seguridad, las transferencias bancarias y otras operaciones que requieren de alta seguridad. Es decir, yo puedo cifrar los mensajes gracias a que conozco la factorización de un número bastante grande. Es un número que parece primo, pero que no lo es: tiene factores que yo conozco. Las técnicas para factorizar ese número que hay hoy en día en el mercado llevan muchísimo tiempo. Si los "malos" supieran factorizar cualquier número grande en un periodo razonable de tiempo, adiós seguridad en internet.
Por eso, fundamentalmente, es importante mantener engrasada la máquina de factorizar números, así como los algoritmos que proporcionan primos grandes. O sea que la pelea por obtener primos grandes, además de una lucha por ver quién tiene la lista más larga, tiene una gran utilidad práctica.
La búsqueda de primos de Mersenne tiene una derivada mucho menos prosaica: el descubrimiento de nuevos números perfectos. Un número perfecto es aquel en el que la suma de sus divisores propios (excluyendo el número) suma el propio número. Los griegos decían "el que es igual a la suma de sus partes". Se tomaron la molestia de ponerles nombre y eso que solo conocían cuatro. El primer número perfecto es 6, tiene 3 divisores si excluimos al propio número: 1, 2 y 3. Si los sumamos 1 + 2 + 3 = 6. Seis es perfecto. El siguiente es 28. Es divisible entre 1 (siempre), 2, 4, 7 y 14 ¿adivináis cuánto da 1 + 2 + 4 + 7 + 14? Exacto, 28.
Cada primo de Mersenne va acompañado de un número perfecto par. Si “2 elevado a p - 1” es primo (y por tanto primo de Mersenne) entonces es perfecto el resultante de:
Vamos a usar la fórmula para encontrar el tercer número perfecto. Para p=5, dos elevado a 5 es 32, menos 1, nos da 31, que es primo, entonces 31·24 = 496 es un número perfecto.
6, 28, 496. Os voy a dar uno más: 8128, que además de la contraseña de mi ordenador (voy a tener que cambiarla) es el producto de 127 (primo de Mersenne) por 64.
127. 64 = 8128
Por último, por si fuera poco, dentro del grupo grande de los números primos, ya raro por sí mismo, existe otro también peculiar, que es el de los primos gemelos, es decir, pares de números primos separados por dos unidades (por ejemplo, 3 y 5, 11 y 13, 41 y 43...).
También se supone que son infinitos, pero se trata de una conjetura, nadie ha podido confirmarlo hasta la fecha. Quizás el momento esté cerca. Hasta ahora, el que más se ha acercado a su resolución es un estudiante de tan solo 26 años del Centro para la Investigación Matemática de la Universidad de Montreal (Canadá), que ha realizado interesantes progresos en este campo y cuyas conclusiones serán pronto publicadas en una revista científica.
¿Lo habéis entendido todo? Pues a mí me cuesta asimilarlo.
Para terminar, os recomiendo una excelente novela: “La soledad de los números primos” de Paolo Giordano, que se ha convertido, hoy por hoy, en el fenómeno editorial más relevante de los últimos años en Italia.
José Antonio Parra Tomás
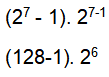
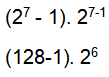
CULTURA
GastronOMÍA
© 2024. All rights reserved.
Creemos de verdad que la gastronomía forma parte de nuestra cultura, y que bien desarrollada también la conforma y nos hace sentir parte de una determinada cultura, en nuestro caso, la mediterránea.
Colaboramos, creamos y apoyamos actividades relacionadas con la cultura. Actividades que sirvan para mejorar la formación y el entretenimiento de nuestros asociados y seguidores. Se trata de contribuir al divertimento en los ratos libres disponibles de la mano de actividades que nos enriquezcan como personas.
contacto
